Face Centered Cubic

• Face Centered Cubic Vs Body Centered Cubic
• Face Centered Cubic Unit Cell Radius Formula
• Face Centered Cubic
• Face Centered
• Face Centered Cubic Lattice
• Face Centered Orthorhombic

Coloring is a enjoyable way to unwind and spark creativity, whether you're a kid or just a kid at heart. With so many designs to choose from, it's easy to find something that matches your style or interests each day.

Unleash Creativity with Face Centered Cubic

Free printable coloring pages are perfect for anyone looking to get creative without needing to buy supplies. Just pick out, print them at home, and start coloring whenever you feel inspired.

Face Centered Cubic

From animals and flowers to mandalas and cartoons, there's something for everyone. Kids can enjoy playful scenes, while adults might prefer detailed patterns that offer a relaxing challenge during quiet moments.

Printing your own coloring pages lets you choose exactly what you want, whenever you want. It’s a simple, enjoyable activity that brings joy and creativity into your day, one page at a time.

Face Centered Cubic

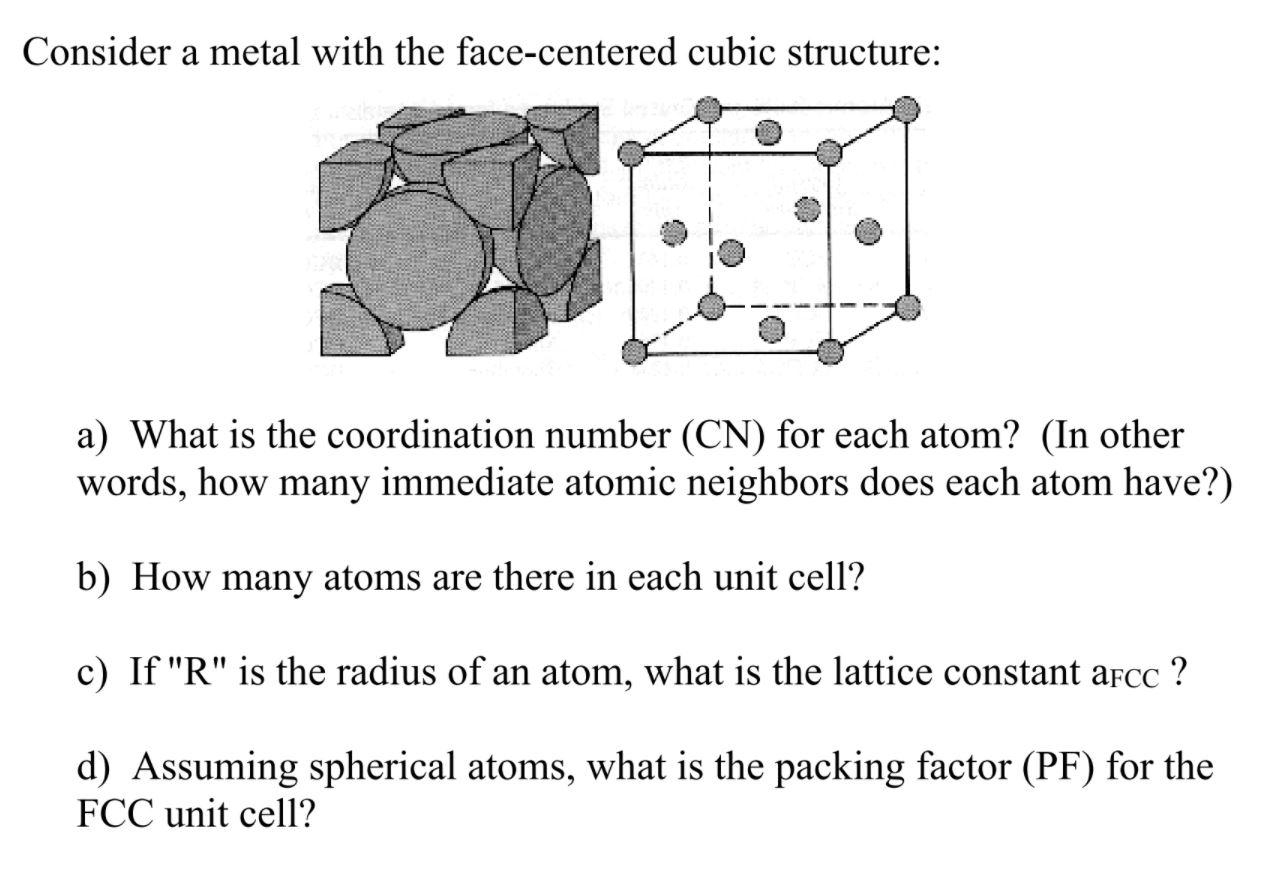
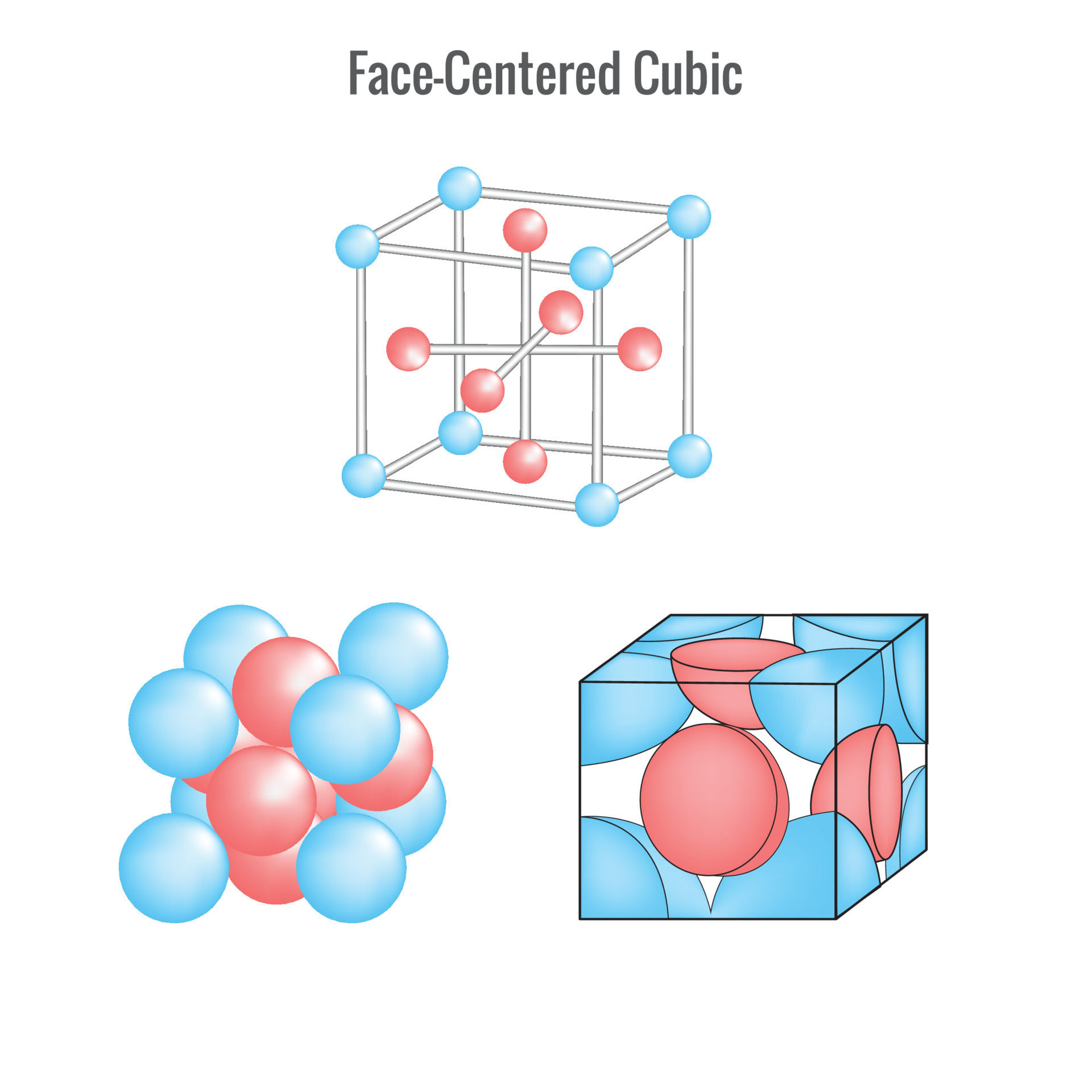
A face centered cubic solid has atoms at the corners and as the name implies at the centers of the faces of its unit cells Atoms in an FCC arrangement are packed as closely together as possible with atoms occupying 74 of the volume This structure is also called cubic closest packing CCP Face-centered cubic (also known as FCC, cF, cubic close-packed or CCP) is the name given to a type of atom arrangement found in nature. A face-centered cubic unit cell structure consists of atoms arranged in a cube where each corner of the cube has a fraction of an atom with six additional full atoms positioned at the center of each cube face.

Face Centered Cubic

Face Centered CubicThis crystal structure is known as face-centered cubic and has atoms at each corner of the cube and six atoms at each face of the cube. It is shown in the figure below. This structure, as well as the next structure we are going to discuss, has the atoms packed as tightly as theoretically possible. Face centered cubic abbreviated cF or fcc Note the term fcc is often used in synonym for the cubic close packed or ccp structure occurring in metals However fcc stands for a face centered cubic Bravais lattice which is not necessarily close packed when a motif is set onto the lattice points

Gallery for Face Centered Cubic